Correlation Analysis in Time Series

Similarity is a kind of correlation, and it's a special case.

Suppose this situation:

Providing a lot of time series with one target time series, we need find the similar series as the target one.

DTW¹ is for Dynamic time wrapping algorithm. DTW could mesure the similarity of two sequence, and it could sussfully handle following situations:

• Different scale of two series
• Time shifting on two series
• Different length of two input series

DTW's time complexity is \(O(n^2)\). The most popular application of DTW is in Voice Recognization, Music Recognization.

Preconditions:

Suppose there are two sequences S1 and S2, and:

• S1 = (a1, a2, a3, a4, …, an)
• S2 = (b1, b2, b3, b4, …, bm)

Which means:

• The length of S1 is n, and the length of S2 is m
• S1 is consits of point a1, a2 …, S2 is consits of point b1, b2 ….
• Generally ai/bi could be a number or a vector

Details:

Generally, the easiest way to compare two series is make both of them have the same length and compared each point. There are some methods to make them have the same length, such as cuting longer one, or scale the shorter one up, etc. However, this kinds of method will lose some features and cannot handling the shifting or scale in a good way, which performs bad in reality.

The way DTW implements is to calcuate a matrix of the two series. As the length of series are n and m respectively, so the matrix's size will be n*m. In the matrix, every element Value(i, j) means the distance between ai(in S1) and bj(in S2). Mathmaticly: $$ Value_{i,j} = Distance(a_i, b_j)$$ In it, distance could be the Euclidean Distance, which is $$ Distance(x, y) = (x - y)^2 $$

As we could see in the expression, the less distance is, the more similar the two values are.

From the view of the whole matrix, we can find out a path in the matrix which goes from (1,1) to (n,m), and if this path has the minimized cumulative distances, we could take the minimized cumulative distances as the Similarity Level. In real application, if we have serveral series, we could use DTW to find the most similar one according to this.

As you can see in the following graph, the left and top lines are the two series, and our target is to find the path like the one in the right-bottom.

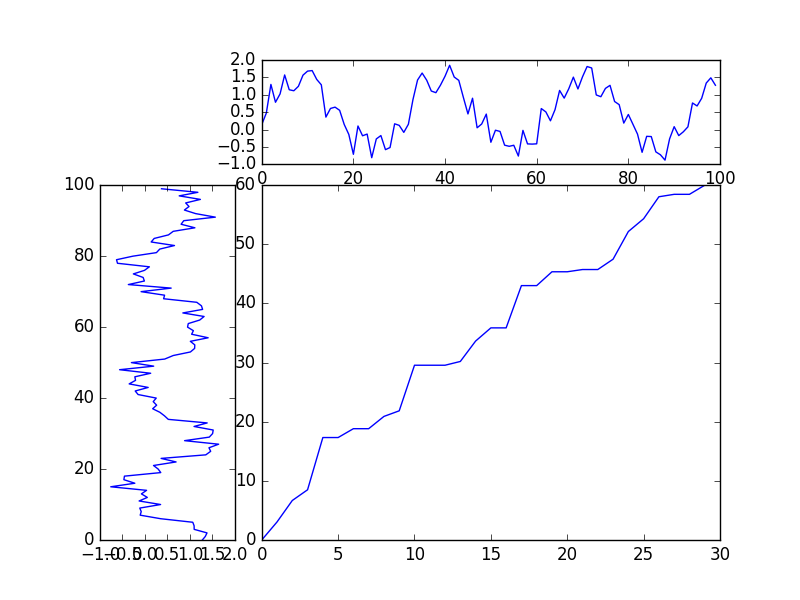
So, how to find out the path?

Let's give the path a defination like this: $$path = (w_1, w_2, w_3, ..., w_k), max(m,n) \le k < m+n-1$$ In it, $$ w_i = v_{p,q}$$ And the cumulative distance(D) of the path could be denoted as: $$D = \sum_{k=1}^K(w_k)$$

\(v_{p,q}\) is the element of the matrix, and i,p,q does not have any relations, we just give some symbols here for convenience.

Next, let's continue to talk about the path, it's noted that the path should satisfy following conditions:

• Boundary: the path should start at (1,1), and ends at (n,m), which is, \(w_1 = v_{1,1}\) and \(w_k =v_{n,m}\)
• Contiunity&Monotonicity: for any \(w_{p-1}=v_{a_1,b_1}\) and \(w_p=v_{a_2,b_2}\), \(w_p\) should be the (up/right/up-right)neighbour elment of \(w_{p-1}\), that's to say, \(0 \le a_2 - a_1 \le 1\) and \(0 \le b_2 - b_1 \le 1\).

There are still a lot paths who satisfy the above conditions, the minimized cumulative distance, the one we want could be denoted as: $$DTW(S1, S2) = min(D_i)$$

To make up for longer distance, the above equation could be improved as: $$DTW(S1, S2) = min(\frac{\sqrt{D_i}}{K})$$

This equation could be figured out with dynamic programing.

Brief Summary:

As we can see, DTW aims to find an path whose cumulative distance is smallest. In fact, different path stands for different "scale up/down" on part of the series, which make the comparesion more flexible. Moreover, once we find the smallest distance, we could get the "similarity level" of the two series, which allows us to decide they are similar or not.

DTW is an excellent algorithm for validating the similarity, but it's a time-consuming algorithm(\(O(m*n)\)) which makes that bad for bussiness application.

Usually in bussiness application, the series to compare are not just two but plenty of pairs. Suppose given one target series, and we are going to find the similar series from the left k serries, the time complexity would be \(O(m*n*k)\).

There are plenty of methods to speed up original DTW algorithm, I will list some popular ones in this part. And those DTW algorithms are improved with different strategy and views, which may inspire you.

As we know there is a cost matrix in original DTW and there have already some constriants on it to limit the search space. The constriants could be found in Section DTW. Following graph illustrate the search space, which is occupied by black color:

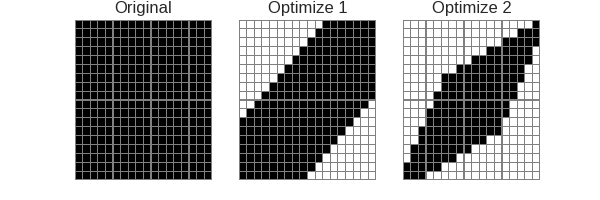
As you could see in the above graph, the rectangle stands for the cost matrix, and the black blocks means the search space to calculate best path.

• in Original DTW algorithm, we have to calculate the whole cost matrix to find the best path.
• with Optimize 1 and Optimize 2, the search space is decreased, so the DTW could be speed up.

Optimize 1 and Optimize 2 is mentioned in Paper², read that paper if you are interested in how it works. But please noted that: the two optimization do limit the search space and speed up the DTW, but it does not guarantee for finding out the best path.

This kind of method takes another view to looked into the path-self. The core thought of this method is to simply(sample) the series first, find one best path and then mapped it to the orignal matrix.

See following graph for illustration:

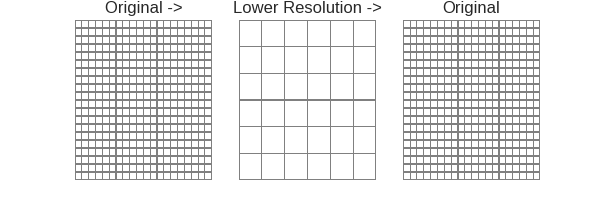
As you can see, this method focus on finding a best path on a lower resolution(sampled) cost matrix, and then maps the path to the original matrix. This do speed up the DTW, but the disadvantage is as the previous one, it does not guarantee the result is the best path.

Read more information about this method, please refer to Paper².

In paper², an integrated methods are provided for DTW algorithm.

The PPMCC³, also caleed PCC or Person correlation coeffcient, is used to test if two variables are linear correlated or not. PPMCC will output a number, which:

• belongs (0, 1]: the two variable are postive correlated
• equals 0: the two variable are not correlated
• blongs [-1, 0): the two variable are negtive correlated

It's noted that:

• PPMCC's time complexity is a \(O(n)\)
• PPMCC requires the variable's length are the same
• PPMCC are usually used in test the linear correlation of two value

The PPMCC is denoted as: $$ \rho_{X,Y} = \frac{cov(X,Y)}{\sigma_X \sigma_Y}$$ $$ = \frac{E[(X - E[X])(Y - E[Y])]}{\sqrt{E[X^2] - (E[X])^2} \sqrt{E[Y^2] - (E[Y])^2}} $$ $$ = \frac{E[XY] - E[X]E[Y]}{\sqrt{E[X^2] - (E[X])^2} \sqrt{E[Y^2] - (E[Y])^2}}$$